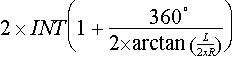
 Version 1.0 - August 16, 1998
Version 1.0 - August 16, 1998
This page gives the solution of the following problem:
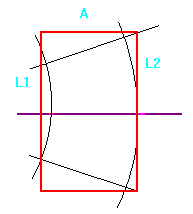
Given a circular corona of external radium R, and a set of veneer sheets of maximum width of L and lengh of H, determine the minimum even number of segments to cover the entire surface, and the value of the internal radium obtained
With reference to the figure at the side, to compute the number of sections we use the same formula as for the case of the computation of the sunburst sections, i.e.:
N = 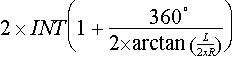
where L=L2 and the corner below is given by: corner=atan(L2/R). The internal radium is therefore computed with the following formula:
The following fields automatically compute the result. Beware that your browser has to support JavaScript.